Radicacion de números reales y sus propiedades

La radicación se define como la operación inversa de la potenciación. La potenciación es una expresión matemática que incluye dos términos denominados: base a y exponente n. Se escribe de la siguiente forma:
Se lee como, “a elevado a n”
Para comprender mejor la definición de radicación, supongamos que nos dan un número a y nos piden calcular otro, de forma tal que, multiplicado por si mismo un número b de veces nos da el numero a. Por ejemplo si queremos averiguar qué número multiplicado por si mismo 2 veces da 196, obtenemos como resultado, 14.

Por esto, las propiedades de la potenciación se cumplen también con la radicación. Para que estas propiedades se cumplan, se exige que el radicando de las raíces sea positivo
RAÍZ DE UN PRODUCTO: La raíz de un producto es igual al producto de las raíces de los factores: \sqrt[n]{{a} \cdot {b}} = \sqrt[n]{a} \cdot \sqrt[n]{b}

RAIZ DE UN COCIENTE:La raíz de una fracción es igual al cociente de la raíz del numerador entre la raíz del denominador:

Raíz de una raíz

Para calcular la raíz de una raíz se multiplican los índices de las raíces y se conserva el radicando: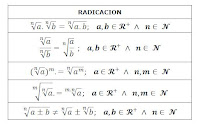 

Resultado de imagen para radicacion de numeros reales

Video:https://www.youtube.com/watch?v=TI19WpBVXuU

Comentarios

Publicar un comentario

Entradas más populares de este blog

Numeros reales

Imagen
El conjunto de los números reales pertenece en matemáticas a la recta numérica que comprende a los números racionales y a los números irracionales. Esto quiere decir que incluyen a todos los números positivos y negativos, el símbolo cero, y a los números que no pueden ser expresados mediante fracciones de dos enteros que tengan como denominador a números no nulos (excluye al denominador cero). Un número real puede ser expresa do de diferentes maneras, por un lado están los números reales que pueden ser expresados con mucha facilidad, ya que no poseen reglas complejas para hacerlo. Estos son los números enteros y los fraccionarios, como por ejemplo el número  67 67  que viene a ser un entero, o también el  3 4 3 4 , que es un número fraccionario compuesto de dos enteros, cuyo numerador es  3 3  y su denominador es  4 4 . Sin embargo, también existen otros números que pueden ser expresados bajo diferentes reglas matemáticas más complejas como números cuyos decimales son infinitos como
Leer más

Potenciacion de numeros reales y notacion cientifica

Imagen
La  operación de potencia  dentro de los diferentes conjuntos númericos respeta determinadas propiedades, en este caso se analizarán para el conjunto de los  números reales . Es importante tenerlas en cuenta porque al manejarlas bien se pueden resolver en forma mas dinámica los ejercicios relacionados que la mayoría de las veces son un dolor de cabeza para los estudiantes de bachillerato en general. Producto de potencias con la misma base : Es otra potencia con  la misma base  y cuyo  exponente  es la  suma de los exponentes . División de potencias con la misma base: Es otra potencia con la misma base y cuyo exponente es la diferencia de los exponentes. Potencia de una potencia : Es otra potencia con la misma base y cuyo exponente es el producto de los exponentes. Producto de potencias con el mismo exponente: Es otra potencia con el mismo exponente y cuya base es el producto de las bases Cociente de potencias con el mismo exponente: Es otra potencia con el mismo exponente y cuya
Leer más